what if? 2
I posted about 2 other books by Randall Munroe a while ago. I think “How to” also was the last book I read. And that was 3 years ago. I feel pretty ashamed. The pandemic and the related social restrictions would have provided the perfect conditions for reading books, but I just wasn’t in the mood. The other day I went to a bookstore and randomly came across “what if? 2”.

Here are a bunch of snippets from the book.
To the question:
If the universe stopped expanding right now, how long would it take for a human to drive a car all the way to the edge of the universe?
the author goes on a tangent trying to put the dimensions of the universe into perspective. I think we humans are really bad at grasping big numbers.
Robin Dunbar famously suggested that the average human maintains about 150 social relationships. The total number of humans who have ever lived is somewhere north of 100 billion. A 1017-year road trip would be long enough to replay the lives of every one of those people in real time—in a sort of unedited documentary—and then rewatch every one of those documentaries 150 times, each time with a different commentary track by the 150 people who knew the subject best.
By the time you finished watching this complete documentary of human perspective, you’d still be less than 1 percent of the way to the edge of the universe, so you’d have plenty of time to rewatch the whole project—each human life with all 150 commentary tracks—100 times before you finally arrived.
From time to time, you come across very short and simple scientific explanations. For example:
A mirage is a reflection of the sky; light from the sky comes down near the surface and then bends up toward your eye, so it looks like it’s coming from the ground.
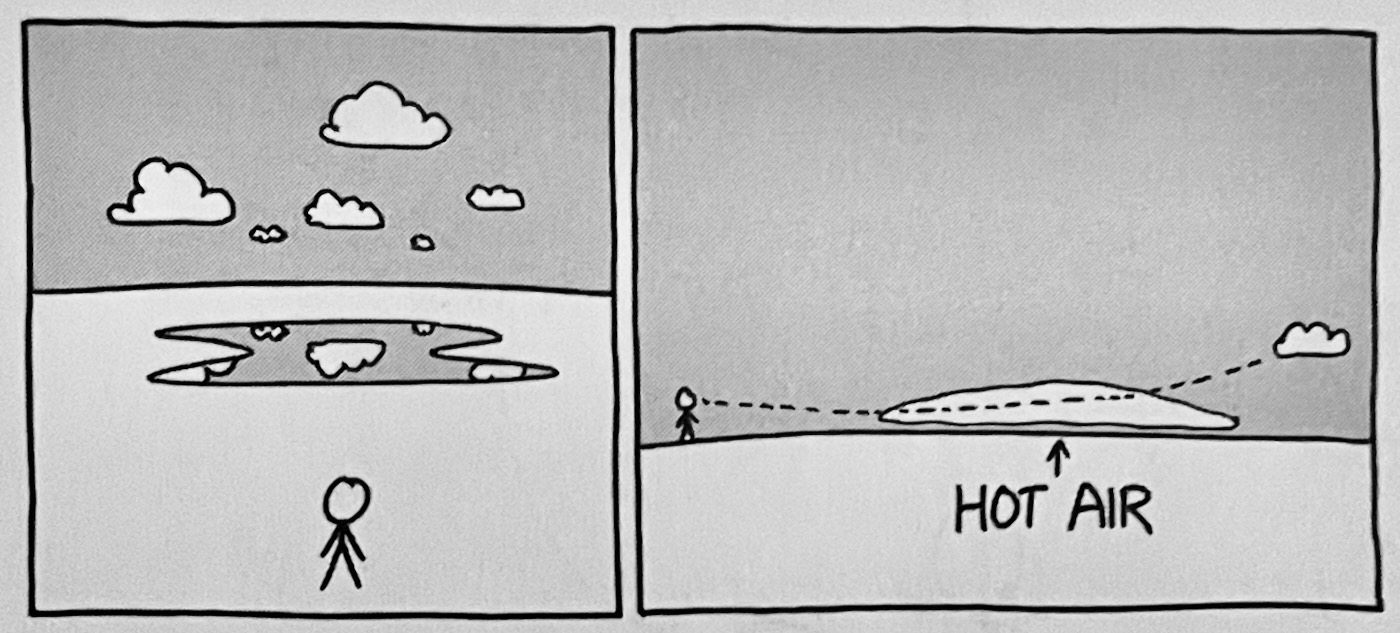
Then there are absurd questions, with obviously equally absurd answers:
How many pigeons would it require in order to lift the average person and a launch chair to the height of Australia’s Q1 skyscraper?
It sounds simple at first, but big numbers are involved again, meaning big problems:
If 600 pigeons can lift you the first 5 meters, then you just need to bring another 600 along with you, like the second stage of a rocket, to carry you the next 5 meters when the first flock gets tired. You can bring another 600 for the 5 meters after that and so on. The Q1 is 322 meters high, so about 40,000 pigeons should be able to get you to the top, right?
No. There’s a problem with this idea.
Since a pigeon can carry only a quarter of its body weight, it takes four flying pigeons to carry one resting pigeon. That means each “stage” will need at least four times as many pigeons as the one above it. Lifting one person may only take 600 pigeons, but lifting one person and 600 resting pigeons would take another 3,000 pigeons.
This exponential growth means that a 9-stage vehicle, able to lift you 45 meters, would need almost 300 million pigeons, roughly equal to the entire global population. Reaching the halfway point would require 1.6 × 1025 pigeons, which would weigh about 8 × 1024 kilograms—more than the Earth itself. At that point, the pigeons wouldn’t be pulled down by the Earth’s gravity—the Earth would be pulled up by the pigeons gravity.
The full 65-stage craft to reach the top of the Q1 would weigh 3.5 × 1046 kilograms. That’s not just more pigeons than there are on Earth, it’s more mass than there is in the galaxy.
Chapter 33 touches one of my favorite topics: family trees. And, again, exponential numbers.
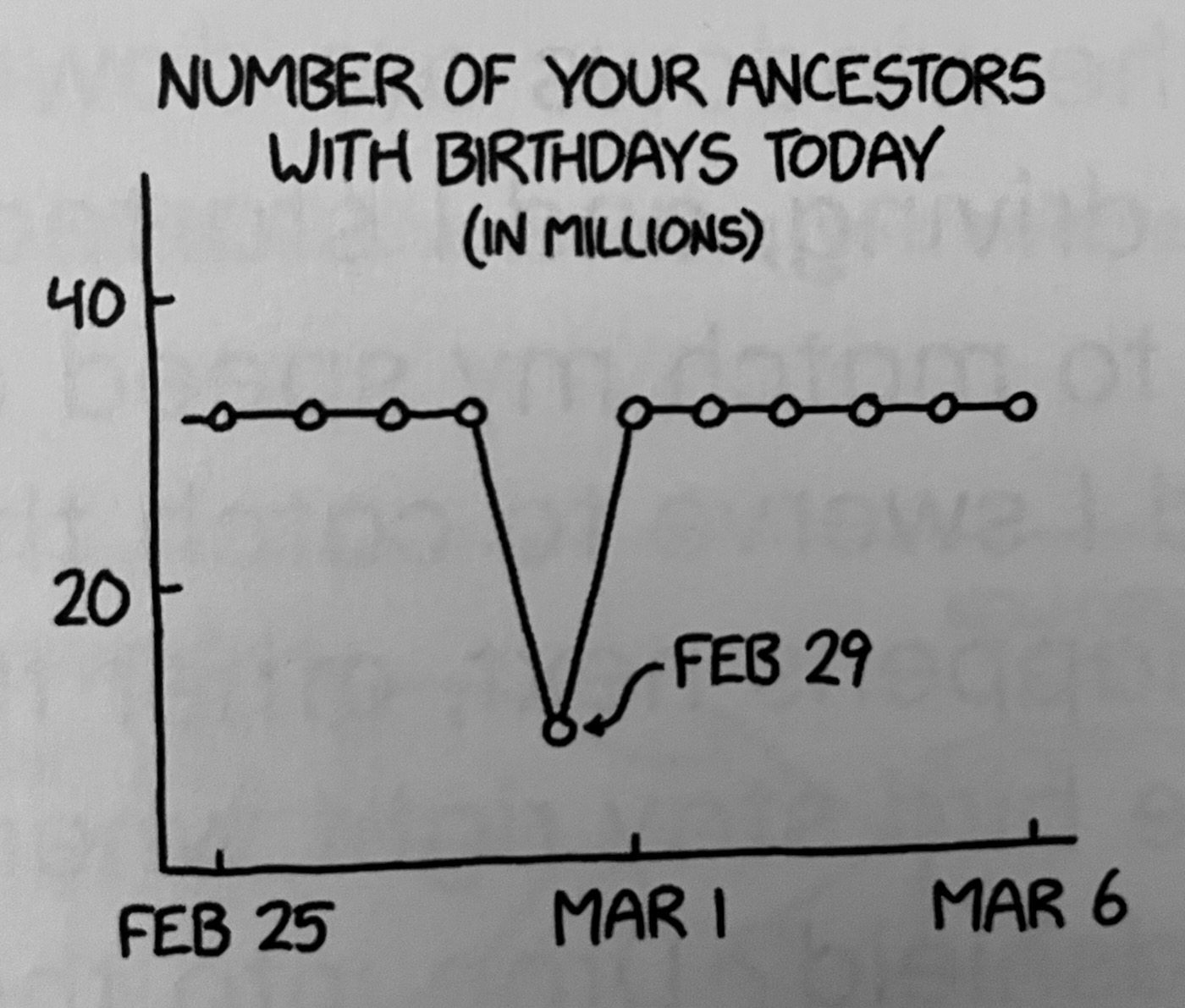
Each of your ancestors represents the merger of two family trees, so more and more people are included as you move further back. It’s possible for your family tree to occasionally shrink as you trace it backward in time—for example, if you had a group of ancestors who were isolated for many generations—but it never dies out. If you follow it back far enough, the relentless doubling means that eventually you’ll reach a date at which all surviving lineages have been absorbed into your family tree. At that point, all the people who left descendants are your ancestors, and you and everyone else have the same set of ancestors.
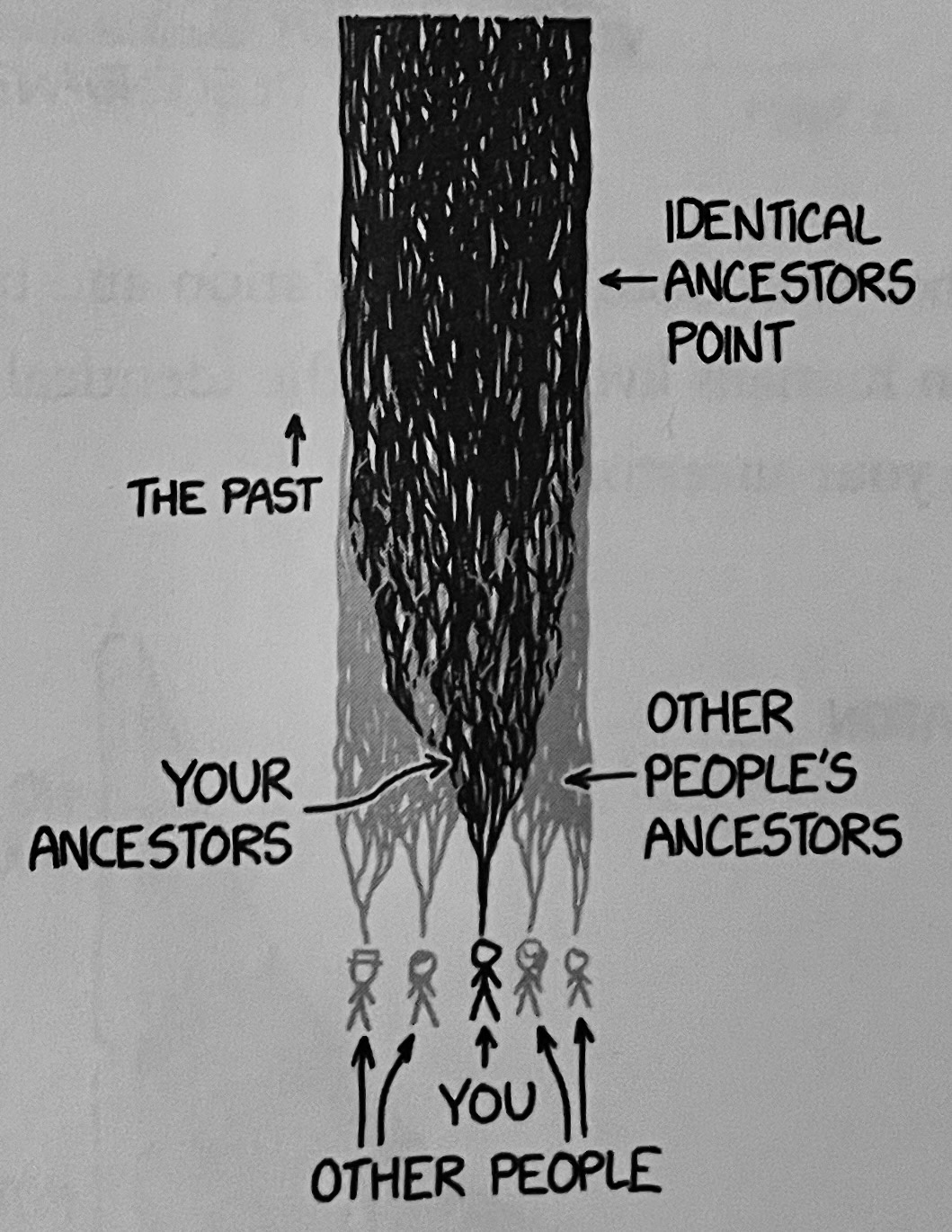
A 2004 simulation by Douglas L. T. Rode and colleagues estimates that the identical ancestors point is likely somewhere between 5000 and 2000 BCE. At that date, everyone who left descendants at all is an ancestor of everyone. Each lineage from that date has either died out or expanded to include all living humans, and so all living humans share the same set of ancestors from that point backward.
Every time people complain about smartphones not being revolutionized year over year, I want to punch them in the face. They don’t realize how crazy the technology in the glass bricks in their pockets is.
Early computers were extremely large by modern standards. ENIAC, the first programmable computer, was taller than a person and 30 meters long. UNIVAC, a commercial computer built a few years later, was a more compact cube shape, but was still the size of a room.
A modern smartphone is smaller than ENIAC or UNIVAC, but it has a lot more digital switches. UNIVAC had a little over 5,000 vacuum tubes packed into its 25 m3 case. An iPhone 12 has 11.8 billion transistors packed into the phone’s 80 mL case, which is about a trillion times more computer per liter.
I like that new unit: computer per liter.
This small graphic made me think of “what is a salad?” or “what is a sandwich?”.
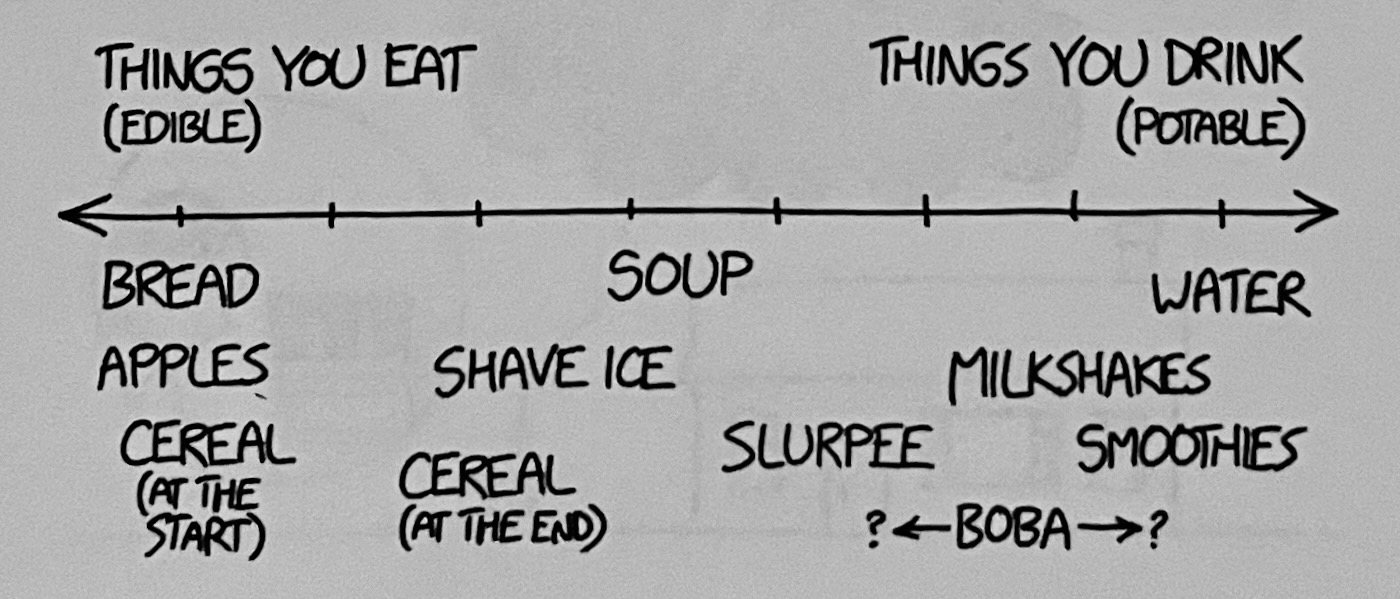
Some English expressions are scientifically wrong:
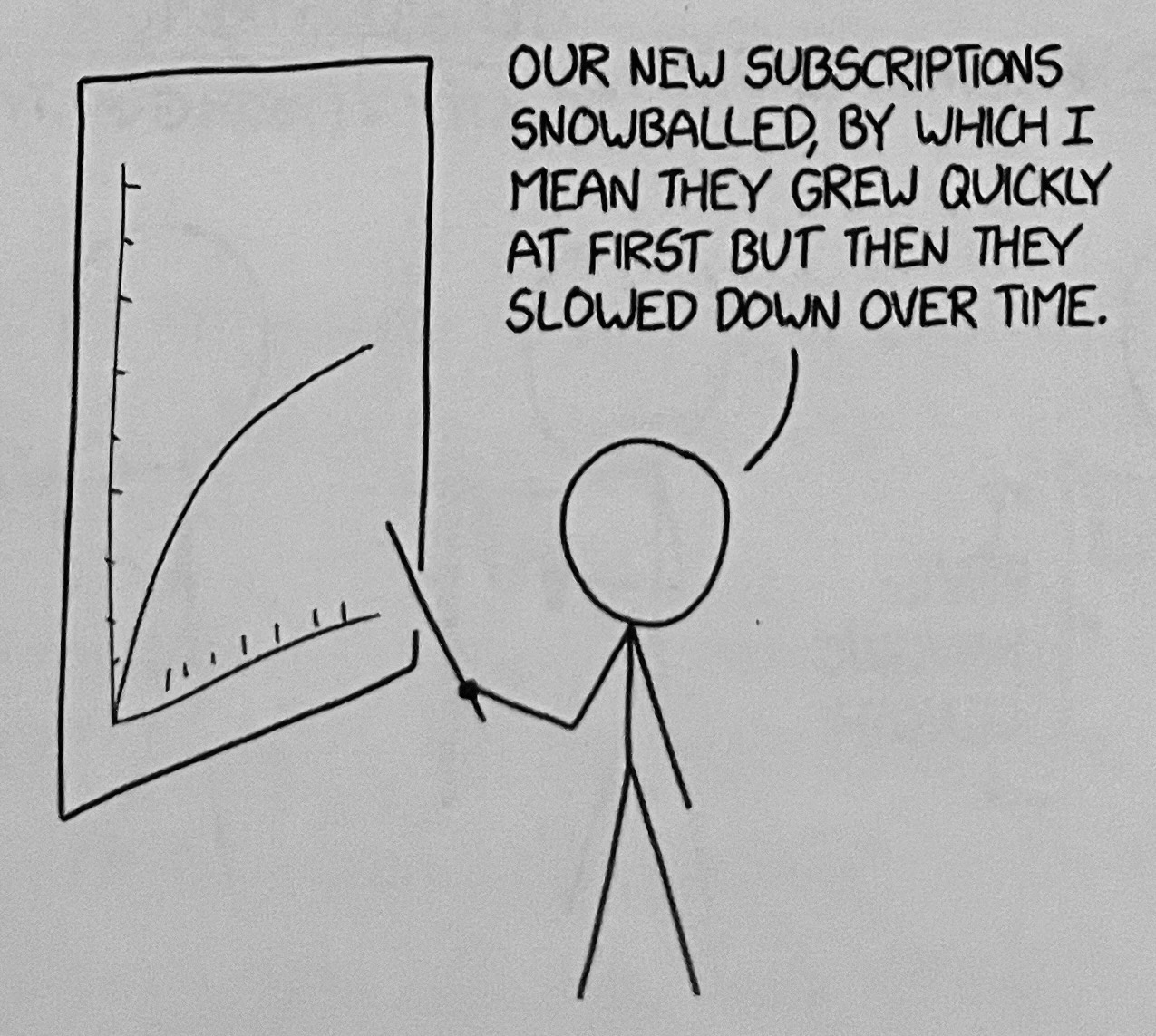
A rolling snowball picks up snow and gets bigger, and a bigger snowball picks up more snow. This may sound like a recipe for some kind of exponential growth, but an idealized snowball’s growth actually slows down over time. It keeps getting bigger and wider, but each new meter it rolls adds less to the diameter. The growth slows because the width of the snowball’s track—and thus the amount of snow it picks up—is proportional to its radius, but the surface area the new snow has to cover is proportional to radius squared, which means that each new clump of snow has to be spread out over more area. People use the word “snowballed” to mean “grew faster and faster,” but in a sense the truth is the reverse.
I think my favorite chapter is the answer to this question:
What if you decided to walk from Austin, Texas, to New York City, but every step you take takes you back 30 days?
I won’t spoil it tough. You’ll have to read the book.
The book also touches random real-world topics I have never thought about, like how to measure snow fall.
If you wait until the end of a snowstorm to measure snow, maybe it will have all squished down, or some of the snow might have melted, so your measurement will be too small.
Instead of waiting until the end of the storm, you can measure the snow in parts. You let some snow fall, measure it, then clear it away and wait for more snow to fall. You have to decide how much snow to clear away. If you wait too long, the snow might become too squished, but if you measure it too often, it will all be light and fluffy and you’ll get a number that’s way too high.
Believe it or not, the National Weather Service has written special guidelines for how often to clear away snow, so everyone can measure it the same way.
If you’re still not sure you want to read the book, or need help navigating the topics, here’s a handy xkcd comic:
And here’s Randall Munroe being interviewed recently in a podcast that I started listening to this year: Dear Hank and John: Juice the cloud, with Randall Munroe